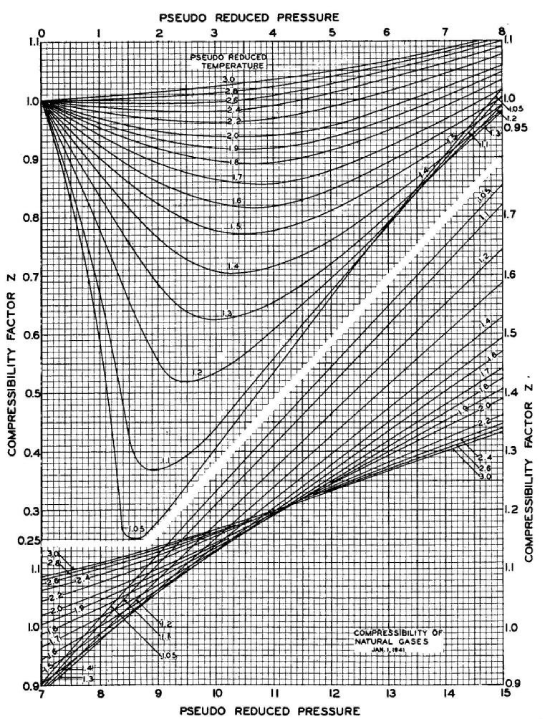
Figure :Standing and Katz’s compressibility factor chart
The z-factor is the ratio of the volume occupied by a given amount of a gas to the volume occupied by the same amount of an ideal gas:
\(z=\displaystyle\frac{V_{actual}}{V_{ideal}}\)
Substituting for \(V_{ideal}\) in the ideal gas equation
\( PV_{actual}=znRT\)
For generalization, the z-factor is expressed as a function of pseudo-reduced temperature and pressure (Trube 1957; Dranchuk et al. 1971; Abou-kassem and Dranchuk 1975; Sutton 1985; Heidaryan et al. 2010).
Dranchuk et al. (1971) defined pseudo-reduced temperature and pressure as the ratio of temperature and pressure to the pseudo-critical temperature and pressure of natural gas, respectively:
\( T_{pr}=\displaystyle\frac{T}{T_{pc}}\,,\;\; P_{pr}=\displaystyle\frac{P}{P_{pc}}\)
The pseudo-critical properties of gas are the molar abundance (mole fraction weighted) mean of the critical properties of the constituents of the natural gas:
\( T_{pc}=\displaystyle\sum_{i=1}^n{y_iT_{c,i}}\,,\;\; P_{pc}=\displaystyle\sum_{i=1}^n{y_iP_{c,i}}\)
\(P\) : Pressure (bar, kPa, psi)
\(P_{pc}\) : Pseudo-critical pressure (bar, kPa, psi)
\(P_{pr}\) : Pseudo-reduced pressure
\(P_{c,i}\) : Gaz karışımındaki i.bileşenin kritik basıncı (bar, kPa, psi)
\(T\) : Temperature (K, R)
\(T_{pc}\) : Pseudo-critical temperature (K, R)
\(T_{pr}\) : Pseudo-reduced temperature
\(T_{c,i}\) : Critical Temperature of Component i in a Gas Mixture (K, R)
\(y_{i}\) : Molar Percentage of Component i in a Gas Mixture
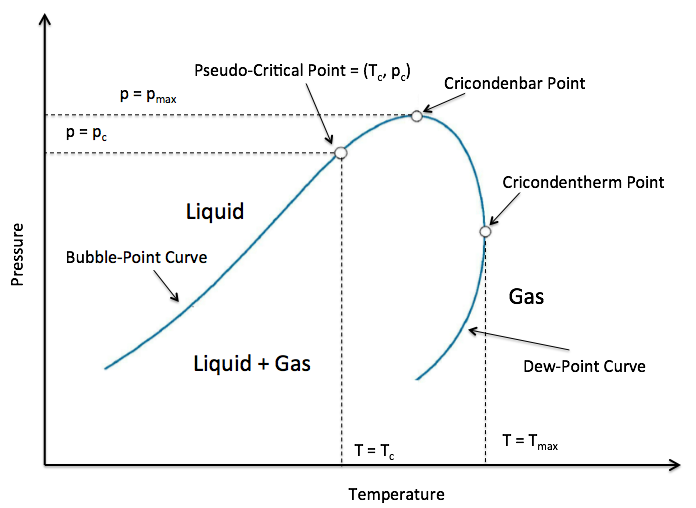
Figure : General Gas P-T Diagram
\(z\) Factor Correlations
The three most popular correlations for calculating the \(z\)-factor are implicit. The three correlations, described in the following subsections, are well known for their accuracies, almost unit correlation of regression coefficients and low maximum errors.
Hall and Yarborough’s correlation (Trube 1957)
Implicit Z-factor correlation model for the natural gas in the wide range of pseudo-reduced temperature \(1.05 \leq T_{pr} \leq 3.0\) and pseudo-reduced pressure \(0.2 \leq P_{pr} \leq 15\)
The \(z\) value is obtained from the formula below.
\( z=\displaystyle\frac{A_1 P_{pr}}{y}\)
The value of \(y\) is the root of the following equation and is obtained by iterating.
\( -A_1 P_{pr} +\displaystyle\frac{y+y^2+y^3-y^4}{(1-y)^3}-A_2y^2+\displaystyle A_3 \displaystyle y^{\displaystyle A_4}=0\)
Below are the values \(A_1\), \(A_2\), \(A_3\), \(A_4\) in the equation.
\( A_1=0.06125t\displaystyle e^{-1.2 \left(1-t\right)^2} \),
\( A_2=14.76t-9.76t^2+4.58t^3 \),
\( A_3=90.7t-242.2t^2+42.4t^3 \),
\( A_4=2.18+2.82t \),
\( t= \displaystyle\frac{1}{T_{pr}} \)
Dranchuk, Purvis and Robinson’s Correlation (Dranchuk et al. 1971)
Implicit Z-factor correlation @model for the natural gas in the wide range of pseudo-reduced temperature \(1.0 < T_{pr} \leq 3.0\) and pseudo-reduced pressure \(0.2 \leq P_{pr} \leq 30\)
and also a specific range of \(0.7 < T_{pr} \leq 1.0\) and \(P_{pr} < 1.0 \):
The \(z\) value is obtained from the formula below.
\(z=\displaystyle\frac{0.27 P_{pr}}{yT_{pr}}\)
The value of \(y\) is the root of the following equation and is obtained by iterating.
\( T_4y^2\left(1+A_{8}y^2\right)e^{-A_{8}y^2}+1+T_1y+T_2y^2+T_3y^5+\displaystyle\frac{T_5}{y}=0 \)
\( T_1=A_1+\displaystyle\frac{A_2}{T_{pr}}+\displaystyle\frac{A_3}{T_{pr}^3} \)
\( T_2=A_4+\displaystyle\frac{A_5}{T_{pr}} \)
\( T_3=\displaystyle\frac{A_5A_6}{T_{pr}} \)
\( T_4=\displaystyle\frac{A_7}{T_{pr}^3} \)
\( T_5=\displaystyle\frac{0.27P_{pr}}{T_{pr}} \)
\(A_1=0.31506237\), \(A_2=-1.04670990\), \(A_3=-0.57832720\),
\(A_4=0.53530771\), \(A_5=-0.61232032\), \(A_6=-0.10488813\),
\(A_7=0.68157001\), \(A_8=0.68446549\)
Brill and Beggs’ compressibility factor (1973)
It is a relation that returns the value of \(z\) directly without iteration.
\( z=A+\displaystyle\frac{1-A}{e^B}+C P_{pr}^D\)
Here,
\( A = 1.39(T_{pr} - 0.92)^{0.5} - 0.36T_{pr} - 0.10,\)
\( B = (0.62 - 0.23T_{pr} )p_{pr} + \left( {\displaystyle\frac{0.066}{{T_{pr} - 0.86}} - 0.037} \right)p_{pr}^{2} +\displaystyle \frac{{0.32p_{pr}^{2} }}{{10^{E} }},\)
\( C = 0.132 - 0.32\log (T_{pr} ),\)
\( D = 10^{F},\)
\( E = 9(T_{pr} - 1)\;,\)
\( F = 0.3106 - 0.49T_{pr} + 0.1824T_{pr}^{2}\)
Dranchuk and Abou-Kassem’s correlation (Abou-kassem and Dranchuk 1975)
Implicit Z-factor correlation @model for the natural gas in the wide range of pseudo-reduced temperature \(1.0 < T_{pr} \leq 3.0\)
and pseudo-reduced pressure \(0.2 \leq P_{pr} \leq 30\) and also a specific range of \(0.7 < T_{pr} \leq 1.0\) and \(P_{pr} < 1.0 \):
The value of \(z\) is obtained from the following formula.
\(z=\displaystyle\frac{0.27 P_{pr}}{yT_{pr}}\)
The value of \(y\) is the root of the following equation and is obtained by iterating.
\( R_5y^2\left(1+A_{11}y^2\right)e^{-A_{11}y^2}+R_1y-\displaystyle\frac{R_2}{y}+R_3y^2-R_4y^5+1=0 \)
\( R_1=A_1+\displaystyle\frac{A_2}{T_{pr}}+\displaystyle\frac{A_3}{T_{pr}^3}+\displaystyle\frac{A_4}{T_{pr}^4}+\displaystyle\frac{A_5}{T_{pr}^5} \)
\( R_2=\displaystyle\frac{0.27 P_{pr}}{T_{pr}} \)
\( R_3=A_6+\displaystyle\frac{A_7}{T_{pr}}+\displaystyle\frac{A_8}{T_{pr}^2} \)
\( R_4=A_9 \left( \displaystyle\frac{A_7}{T_{pr}}+\displaystyle\frac{A_8}{T_{pr}^2}\right) \)
\( R_5=\displaystyle\frac{A_{10}}{T_{pr}^3} \)
\(A_1=0.3265\), \(A_2=-1.070\), \(A_3=-0.5339\),
\(A_4=0.01569\), \(A_5=-0.05165\), \(A_6=0.5475\),
\(A_7=0.7361\), \(A_8=0.1844\), \(A_9=0.1056\),
\(A_{10}=0.6134\), \(A_{11}=0.7210\)
Heidaryan, Moghdasi and Rahimi’s Correlation
It is a relation that returns the value of \(z\) directly without iteration.
\(z = \ln \left( {\displaystyle\frac{{A_{1} + A_{3} \ln (P_{pr} ) + \displaystyle\frac{{A_{5} }}{{T_{pr} }} + A_{7} \left( {\ln (P_{pr} )} \right)^{2} + \displaystyle\frac{{A_{9} }}{{T_{pr}^{2} }} + \displaystyle\frac{{A_{11} }}{{T_{pr} }}\ln (P_{pr} )}}{{1 + A_{2} \ln (P_{pr} ) + \displaystyle\frac{{A_{4} }}{{T_{pr} }} + A_{6} \left( {\ln (P_{pr} )} \right)^{2} +\displaystyle \frac{{A_{8} }}{{T_{pr}^{2} }} + \displaystyle\frac{{A_{10} }}{{T_{pr} }}\ln (P_{pr} )}}} \right)\)
\(\begin{array}{ l l l }
\rlap{\text{Tablw: Constants of the Heidarian correlation}}\\
\hline
& P_{pr} \leq 3\; & P_{pr}>3\; \\
\hline \hline
A_1 & \;\;\;2.827793 & \;\;\;3.252838 \\
A_2 & -4.688191x10^{-1} & -1.306424x10^{-1} \\
A_3 & -1.262288 & \;\;\;6.449194x10^{-1} \\
A_4 & -1.536524 & -1.518028 \\
A_5 & -4.535045 & -5.391019 \\
A_6 & \;\;\;6.895104 × 10^{-2} & -1.379588 × 10^{-2} \\
A_7 & \;\;\;1.903869 × 10^{-1} & \;\;\;6.600633 × 10^{-2} \\
A_8 & \;\;\;6.200089 × 10^{-1} & \;\;\;6.120783 × 10^{-1} \\
A_9 & \;\;\;1.838479 & \;\;\;2.317431 \\
A_{10} & \;\;\;4.052367 × 10^{-1} & \;\;\;1.632223 × 10^{-1} \\
A_{11} & \;\;\;1.073574 & \;\;\;5.660595 × 10^{-1} \\
\hline
\end{array} \)
Kareem \(z\)-faktor Correlation (2016)
\(z = \displaystyle\frac{{ DP_{pr} (1 + y + y^{2} - y^{3} )}}{{\left( {DP_{pr} + Ey^{2} - Fy^{G} } \right)(1 - y)^{3} }}\)
\(y = \displaystyle\frac{{ DP_{pr} }}{{\left( {\frac{{1 + A^{2} }}{C} - \displaystyle\frac{{A^{2} B}}{{C^{3} }}} \right)}} ,\)
Here,
\(t = \frac{1}{{T_{pr} }}\),
\(A = a_{1} te^{{a_{2} (1 - t)^{2} }} P_{pr}, \)
\( B = a_{3} t + a_{4} t^{2} + a_{5} t^{6} P_{pr}^{6}, \)
\( C = a_{9} + a_{8} tP_{pr} + a_{7} t^{2} P_{pr}^{2} + a_{6} t^{3} P_{pr}^{3},\)
\(D = a_{10} te^{{a_{11} (1 - t)^{2} }}, \)
\(E = a_{12} t + a_{13} t^{2} + a_{14} t^{3}, \)
\( F = a_{15} t + a_{16} t^{2} + a_{17} t^{3},\)
\(G = a_{18} + a_{19} t \)
\(\begin{array}{ l l }
\rlap{\text{Table:Constants of Kareem correlation}}\\
\hline \hline
a_1 = 0.317842 & a_{11}= -1.966847 \\
a_2 = 0.382216 & a_{12} = 21.0581 \\
a_3 = -7.768354 & a_{13}= -27.0246 \\
a_4 = 14.290531 & a_{14}= 16.23 \\
a_5 = 0.000002 & a_{15} = 207.783 \\
a_6 = -0.004693 & a_{16} = -488.161 \\
a_7 = 0.096254 & a_{17}= 176.29 \\
a_8 = 0.166720 & a_{18}= 1.88453 \\
a_9 = 0.966910 & a_{19}= 3.05921 \\
a_{10}= 0.063069 & \\
\hline
\end{array}
\)
Bibliography :
New explicit correlation for the compressibility factor of natural gas: linearized z-factor isotherms
Lateef A. Kareem, Tajudeen M. Iwalewa & Muhammad Al-Marhoun